Create a LabVIEW VI that will estimate the value of \(\pi\) using the Monte Carlo technique described below.
You will use a combination of geometry and random numbers to estimate \(\pi\). Within a while loop that will run until you press a STOP button, repeatedly create two random numbers each ranging from \(-1\) to \(1\) and treat these numbers as an (x, y) coordinate pair. Repeat this process many times and count how many of your coordinates would lie inside a circle of radius \(1\). Since the numbers are random, the number \((n)\) of coordinate pairs that lie inside the circle of radius \(1\) divided by the total number \((N)\) of coordinate pairs selected should be proportional to the ratio of the area of a circle of radius \(1\) divided by the area of a \(2 \times 2\) square.
$$\frac{n}{N}=\frac{\textrm{Area of circle of radius 1}}{\textrm{Area of a }2 \times 2\textrm{ square}} = \frac{\pi (1)^2}{4}$$
Solving, we have the following equation that can be used to estimate \(\pi\):
$$\pi = 4\frac{n}{N}$$
Of course the estimate will be better as \(N\) gets larger but you cannot get more and more digits of precision by continuing the let the simulation run. There are built in VIs that will allow you to create a random number within a range. Of course you should expect to need to maintain a shift register with the values of for the quantities \(n\) and \(N\) and then use these values to estimate your value for \(\pi\).
- Make an XY graph that shows the points that lie inside the unit circle and outside the unit circle as two separate traces.
- Reset the computation on the first call of the VI or if a user presses a RESET Boolean button.
- Allow the user to adjust the speed of placing new points on the loop from 1 ms to 100 ms per point. The default value should be 1 ms. The image below shows this with a logarithmic scale but that isn’t required.
Here is a graphic that shows what your final result show look like.
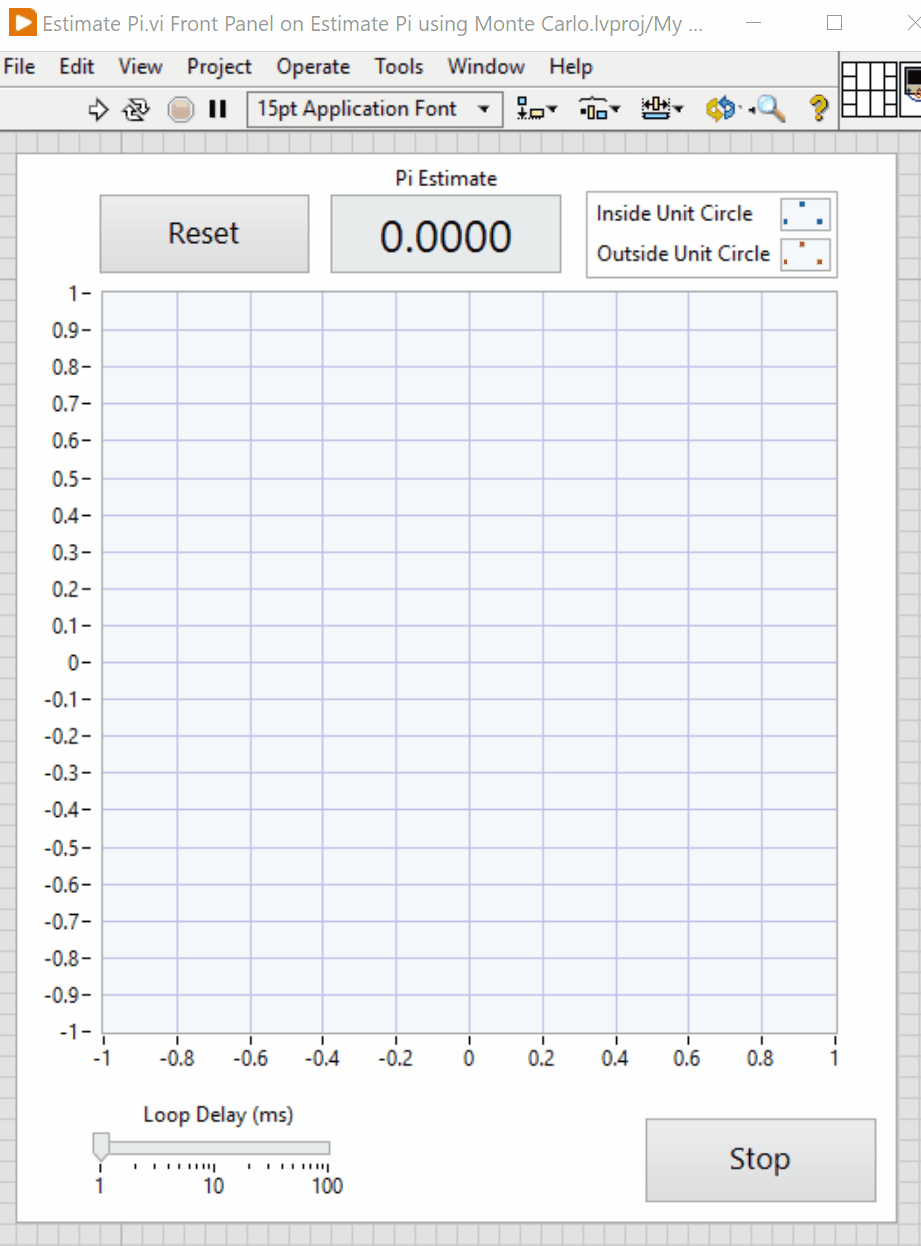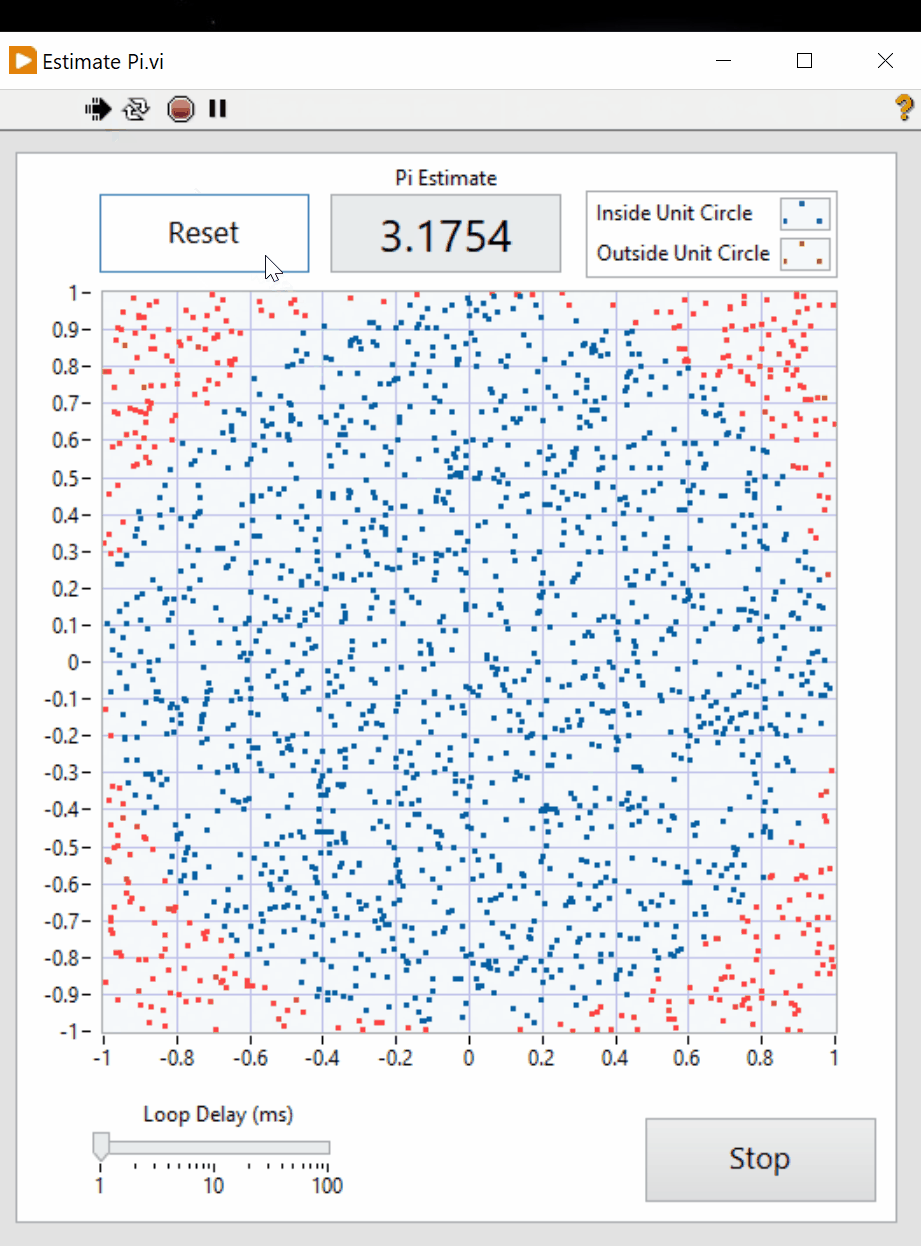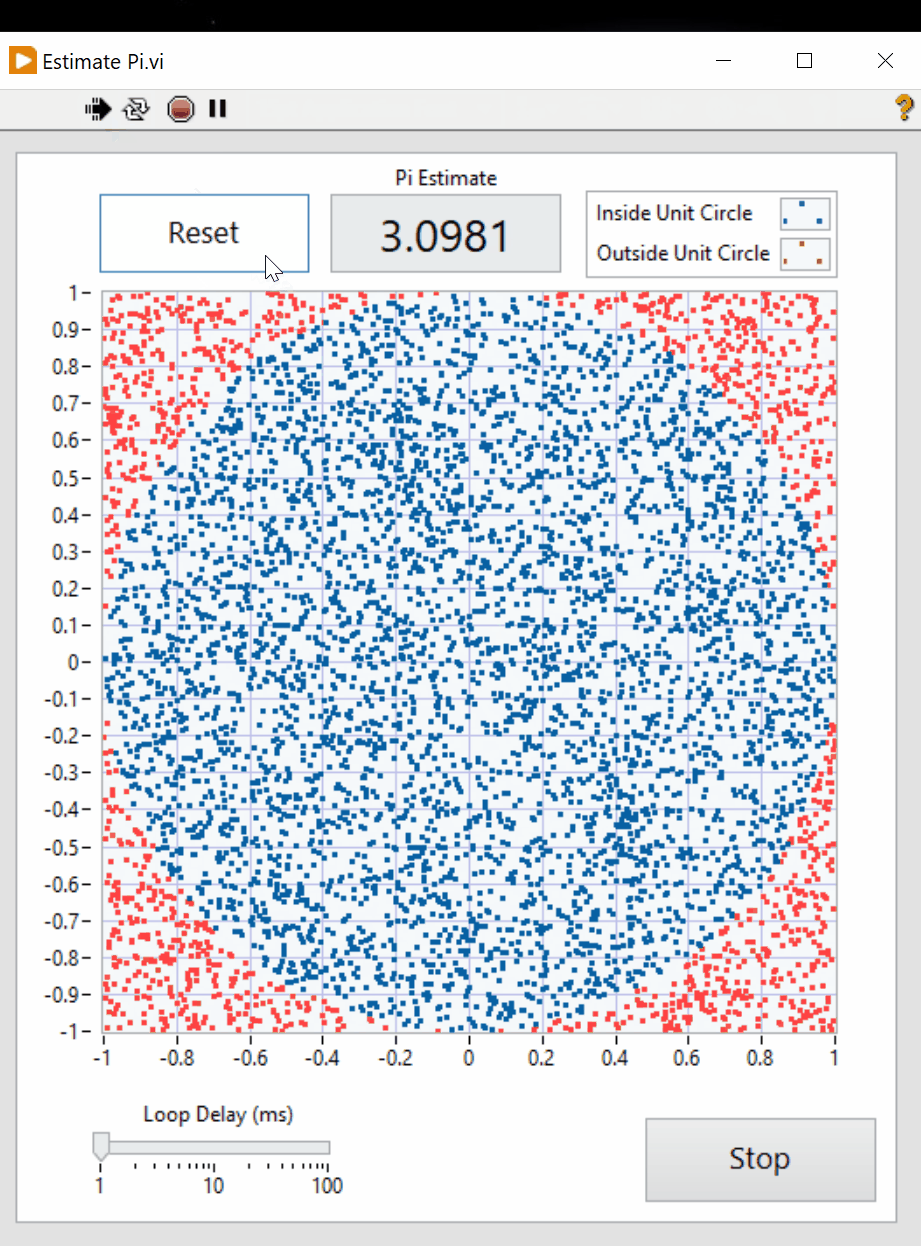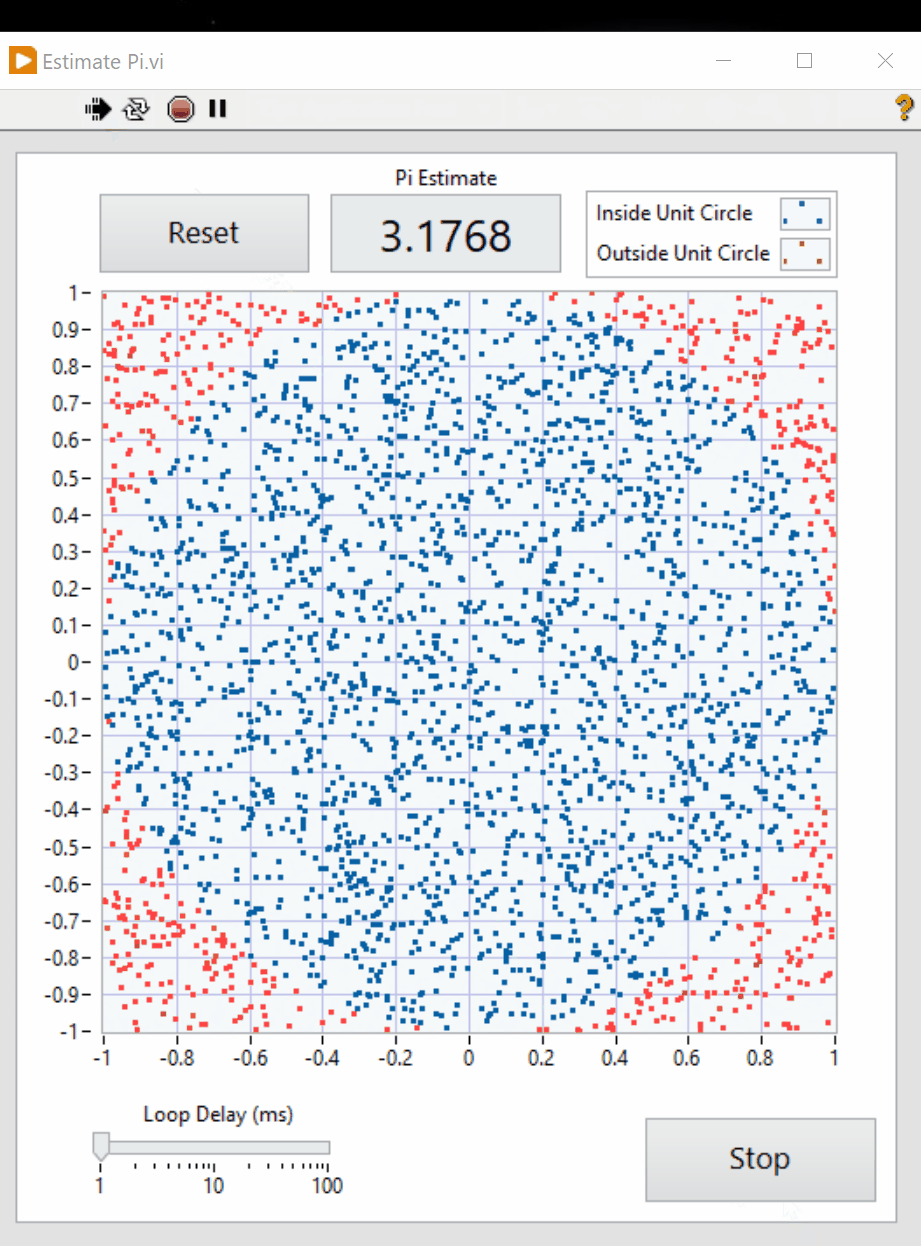
Scoring:
- Functionality – 25 points
- Style – 15 points
- Documentation – 10 points
How to Submit:
Submit your completed code in a new folder inside your SVN dropbox before Midnight, Saturday, January 8, 2022.

