Assignment 09A - For
Introductory Spreadsheet Users
After discussing some of the basic concepts of spreadsheet
use we will create a spreadsheet in class that computes the average value and
standard deviation of a set of N different measurements. If the
measurements are identified by the variables x1, x2,
x3, ... , xN then the average value of these
measurements is given by
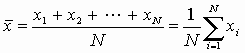
and the standard deviation of the measurements is given by
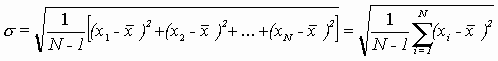
Assignment 09B - For
Experienced Spreadsheet Users (and all currently in University Physics)
The molar heat capacity, C, of a material is defined
as the amount of heat required per mole of the material per unit temperature
change to raise the temperature of the material. If you have encountered heat
capacity (or specific heat) in an introductory chemistry or physics class you
probably assumed that the heat capacity was constant for a given material. This
is true of most materials at temperatures near room temperature. However, at
very low temperatures the heat capacity of a material is not constant – it
varies with temperature.
The heat capacity of a metal at very low temperatures can be
described by a contribution from the electrons in the metal that is linear with
temperature and a contribution from atomic vibrations that varies as the cube of
the temperature. In other words, the following expression can be written for the
heat capacity as a function of temperature:
where A and B are constants (depending on the material) that
describe the strength of the electron contribution and atomic vibration
contribution to the heat capacity respectively.
If the above equation is divided by temperature we have
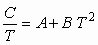
Then a graph of the heat capacity divided by temperature (C/T)
versus the square of the temperature (T2) would be a linear
relationship with slope B and y-intercept A.
The data below represent experimental measurements of the
heat capacity of Copper (Cu) as a function of temperature from 0.2 K (Kelvin) to
1.7 K. The units of the heat capacity are millijoules per mol per Kelvin,
or mJ/(mol K).
-
Enter the data into a new spreadsheet.
-
Create a column titled T
Squared whose values are the square of the temperature.
-
Create a column titled C/T
(EXP) whose values are the heat capacity divided by the
temperature.
-
Use the SLOPE and INTERCEPT functions in
Microsoft excel to compute the slope and intercept of a graph of C/T
versus T. The Y-Values will be the C/T
(EXP) column. The X-Values will be the T
Squared column. The slope will be the parameter B
in the above equation and the intercept will be A.
-
Create a column that uses the above equation and
your values for A and B to compute the
fitted values of C/T. Call this column C/T
(FIT).
-
You should submit a printout of your spreadsheet
showing the columns Temperature, HeatCapacity,
T Squared, C/T
(EXP) and C/T (FIT).
-
As a bonus, make a graph showing both C/T
(EXP) versus T Squared
and C/T (FIT) versus T
Squared.
|
Temperature |
Heat Capacity |
| K |
mJ / (mol K) |
| 0.2 |
0.141 |
| 0.5 |
0.362 |
| 0.6 |
0.430 |
| 0.8 |
0.582 |
| 0.9 |
0.660 |
| 1.0 |
0.749 |
| 1.1 |
0.819 |
| 1.3 |
1.001 |
| 1.5 |
1.202 |
| 1.6 |
1.312 |
| 1.7 |
1.415 |